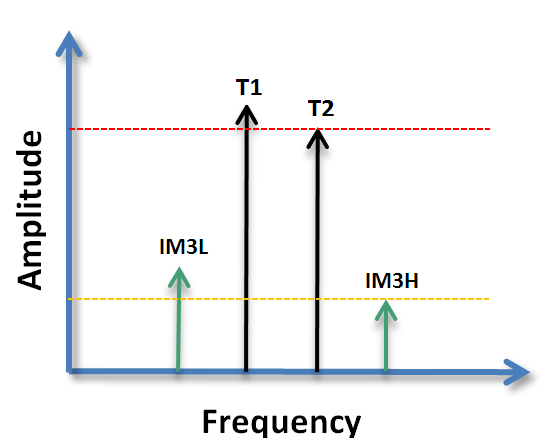
IP3 (3rd order intercept point) is a theoretical figure of merit describing the 3rd order distortion performance of a circuit. Often it is assumed that the tones are at the exact same level and the IM products are identical. In reality, this is typically not the case. Third order distortion causes multiple unwanted products. The most prominent during a two tone test would be the intermodulation products at 2f1-f2, 2f2-f1 and third harmonics at 3f1 and 3f2. The most bothersome in a relative narrowband system would be the intermodulation products, as they often appear in band. See derivation below the calculator.
Low freq.
High freq.
1. Select calculation, IP3 or IM3 products
2. Enter the levels and frequencies if required, then press the Calculate button to compute the third order intercept point (IP3), or the IM3 products.
The yellow boxes indicate results and are read only. Note! The two tones (and IM3 products) do not have to be equal.
Changing the values in the input cells will change the results and graph in real time after the form has been sumbitted with the initial values.
Let's assume we have a two tone signal being applied to a system that has third order distortion. Tone 1 has amplitude of v1 @ frequency = f1, and tone 2 has amplitude of v2 @ frequency f2. Let's also assume f1<f2. The input signal can be represented as
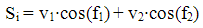
Adding in 3rd order distortion, we have
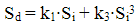
Derivation of the distortion products can be done by cubing the input signal, and isolate the intermodulation products:
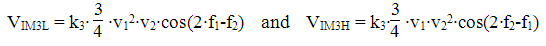
The expression for the distorted signal can be represented as
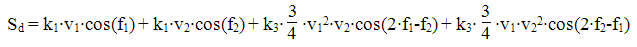
The third order intercept point is defined as the theoretical point of where the intermodulation distortion products are equal to the desired tones, which is expressed below (choosing the tone and intermodulation product that cancels out one of the tones).
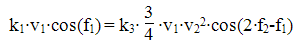
As we are only interested in the levels, we can ignore the cosine terms going forward. Solving for the ratio between k1 and k3, and we can define k1 = 1, we have an expression for the relationship between the third order coefficient k3 and the intercept point voltage of v2, which we can rename to vIP3.
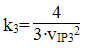
Using the remaining two products, we can express the ratio between the tone at f2 and the low side intermodulation product as
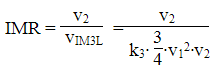
Substituting for k3 based on the previous derivation, we have an expression for the InterModulation Rejection (IMR) voltage ratio based on the tone level v1 at f1 and the IP3 level.
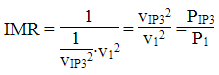
Typically we want to describe the IMR as a power ratio, so let's square both sides
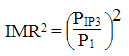
This is now in linear power, we can now convert it to log (dB) units:
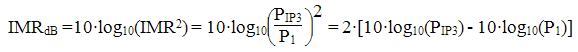
We then end up with the familiar relationship:
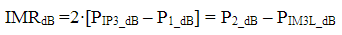
The expression can also be derived using the opposite tone and intermodulation product, which now allows us to calculate the IP3 based on uneven tones and IM3 levels.