OFDM is used in a number of communication and networking standards, including LTE, Wi-Fi, DOCSIS cable modems, MOCA home networking etc. As OFDM typically have a large number of carriers, the impact of 3rd order distortion gets a bit more complicated to evaluate as the number of distortion product combinations are very high. This calculator and article specifically addresses the distortion generated from 3 tones, which is the basis for determining the impact of a multicarrier OFDM signal. See derivation below the calculator.
Tone 1
Tone 2
Tone 3
1. Select calculation, IP3 or xmod/IM3 products
2. Enter the levels and frequencies if required, then press the Calculate button to compute the third order intercept point (IP3), or the cross modulation and IM3 products.
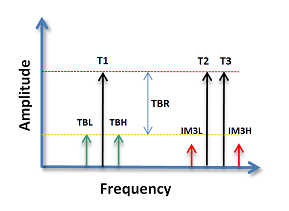
The yellow boxes indicate results and are read only. Note! Enter the tones such that tone 1 is the lowest and tone 3 is the highest frequency. The cross modulation products are only calculated for tone 1, and the IM3 products are only calculated around tone 2 and 3.
Changing the values in the input cells will change the results and graph in real time after the form has been sumbitted with the initial values. For IP3 calculations, default frequencies are assinged as it it not important for the calculation of the interept point.
Acronyms:
Let's take Wi-Fi as an example, which uses OFDM modulation. The 801.11n and ac standard utilize 56 carriers (52 data, 4 pilot). The IFFT is 64 points, and the channel bandwidth is 20 MHz, which leaves the carrier spacing at 20 MHz / 64 = 312.5 kHz. The symbol time without guard bands is then 1 / 312.5 kHz = 3.2us. The carrier spacing must be the reciprocal of the symbol time for the carriers to be orthogonal.
The practical impact of the large number of tones with respect to 3rd order distortion is not straight forward to assess, as the number of distortion products become significant very quickly as the number of carriers increase. 3rd order distortion of interest are combinations of two tones as well as 3 tones. The number of combinations of 2 and 3 tones can be found evaluating the combination method of determining how many unique elements of 2 and 3 exist in a collection of 56.
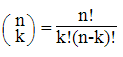
Combinations of 2 tones out of 56, at frequencies 2·f1-f2 and 2·f2-f1:
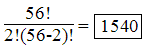
Combinations of 3 tones out of 56, at frequencies ±f1±f2±f3:
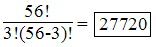
Combinations of three tones will generate products where the beat between two tones will modulate a third tone, this is known as cross modulation. Next is to determine the maximum bandwidth and the levels of the products from 2 and 3 tones.
For the 2 tone case, the widest bandwidth is when the highest and lowest frequency carriers generate IM3 products. If f2 is the highest frequency and f1 is the lowest frequency of the OFDM carriers, the BW = f2 - f1. The bandwidth of the distortion products are then
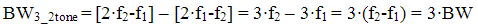
For the 3 tone case, the widest bandwidth is when the highest and lowest frequency carriers generate cross modulation products from the closest and most distant carriers. If f3 is the highest frequency, f1 is the lowest frequency, and f2 is the second highest frequency of the OFDM carriers, the BW = f3 - f1. The carrier spacing is fc, which means f2 = f3-fc for the highest frequency distortion product. Highest frequency cross modulation product is then
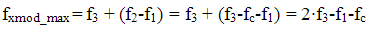
Similarly for the lowest distortion product, now f2 = f1+fc, resulting in
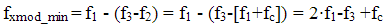
The bandwidth of the distortion products are then
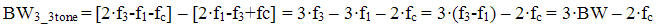
The distribution of the products will not be uniform in either case, as the probability for products being generated in the center is much higher than products being generated at the edges.
The next part is to examine the levels of the various 3rd order products. From the previous 2 tone derivations, we know the IM3L and IM3H products are
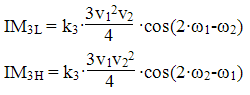
To determine the cross modulation products, we can utilize a similar approach, now just with three tones vs two:
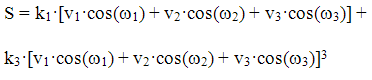
From the 3rd order expansion the two in-band products (triple beats, TB) of interest will be
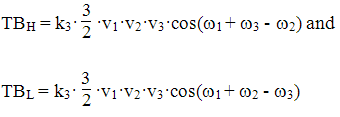
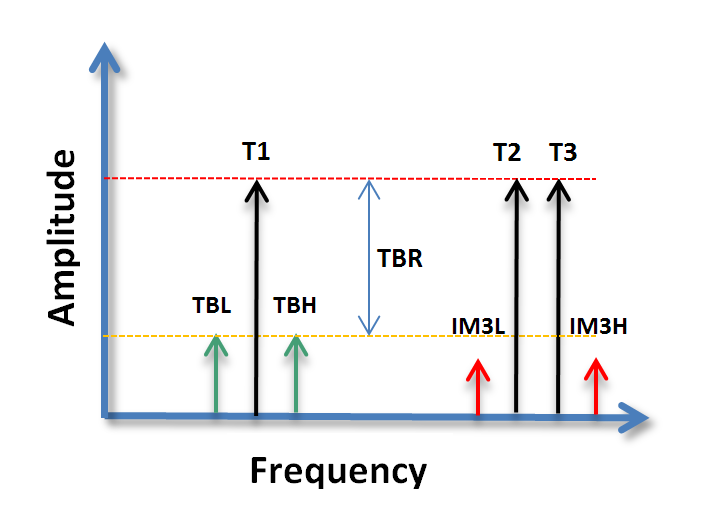
Assuming that all tones in the undistorted signal are at the same level, notice the triple beat products (cross modulation from 3 tone combinations) are twice as large as the IM3 products from 2 tone combinations. Also realizing that there are 27720 combinations of 3 tones, each producing 6 cross modulation products, vs only 1540 two tone combinations, each only producing 2 intermodulation products. The total difference for the aggregate distortion from cross modulation products vs intermodulation products are 6 dB + 10·log10[27720·6 / 1540·2] = 23.3 dB, assuming the distribution is similar. Nevertheless, for all practical purposes, the main concern will be the cross modulation products.
The relationship between k3 and IP3 has been derived earlier, so knowing that
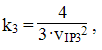
the relationship between the a tone and the associated cross modulation products can be derived. On the figure this is referred to as the Triple Beat Ratio, or TBR.
The voltage ratio is then
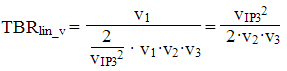
Note that the TBR is not dependent on the victim tone, only the levels of the two tones from which the cross modulation is caused. The power ratio can be found by squaring the voltage ratio, IP3 is the power intercept point
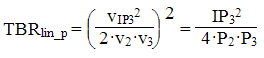
Convert to decibel, using that P_dB = 10·log10(P), log(xy) = log(x)+log(y) and log(x/y)=log(x)-log(y):
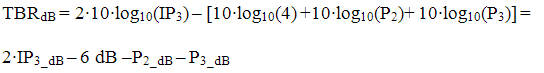
If the all the carriers are at the same level, PT = P2 = P3 we can simplify to
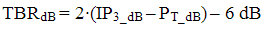
Circling back to the IMR3 derived previously, the 6 dB difference between TBR and IMR3 is clear. Another noteworthy aspect of the TBR is that the products will be symmetric on both sides of the modulated tone/carrier, unlike the IM3 products.
One can also use this derivation to calculate the IP3 from a 3 tone test, which in many cases can be a more realistic scenario than using only two tones. The IP3 derived from the 3 tone test is either
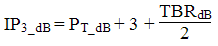
in the case when the carriers are at the same level, or
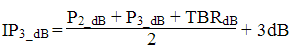
in the case when the carriers are not same level.